
Статистика занимается не только обработкой накопленных данных, но и нахождением тенденций в различных парных показателях, которые связаны друг с другом, что успешно решается применением инструмента «ряды динамики в статистике».
Классическим примером является изменение каких-либо показателей за определенный промежуток времени, что в конце концов сводится не к изучению попарной зависимости (показатель время), а к изучению изменений показателей в динамике.
Понятие о рядах динамики
Строгое понятие для ряда динамики обозначено в статистике так.
Динамические ряды (иными словами ряд динамики или временной ряд) – это распределенные в увеличивающемся порядке дискретных значений выбранного статистического параметра за последовательные временные промежутки.
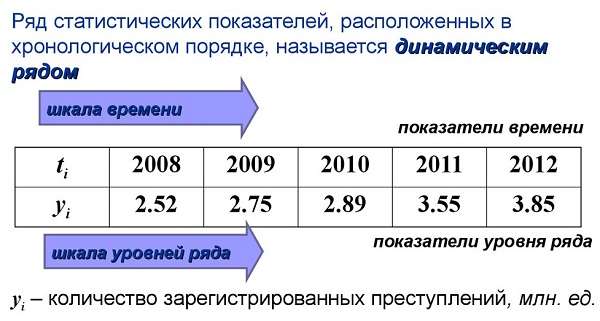
Если рассмотреть динамический ряд, будет очевидно, что он наполнен данными в формате y1t1, y2t2, y3t3…yntn. Применительно к временному ряду, значением у будет называться «уровень ряда», при этом первый член ряда (у1) называется базисным (начальным) уровнем, а уn – конечным уровнем. Через обозначение t будет обозначаться временной показатель, который соответствует каждому из уровней ряда.
При построении графической зависимости временного ряда, функция будет иметь вид t(y), где по оси y (ординат) будут отложены значения уровней ряда (параметр у), а по оси х (ось абсцисс) будут отложены временные значения параметра t.
Пример ряда динамики и его характеристика
В качестве примера, рассмотрим следующий ряд.
Таблицу можно озаглавить так: «Годовой выпуск препарата «Ибупрофен» в 2013-2018гг. в млн. уп.»
| Год | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| Годовой объем выпуска, млн. уп. | 88,1 | 91,3 | 96,5 | 99,3 | 101,8 | 100,7 |
В данном ряду можно обнаружить присутствие следующих показателей:
- имеется показатель t, которому соответствует строка «Год», содержащая информацию о периоде, за который выпускался препарат «Ибупрофен»,
- имеется показатель у, который показывает годовой объем производства препарата «Ибупрофен»,
- показатели t и у соотнесены.
На основании изложенного, можно сделать вывод, что перед нами находится временной ряд.
Виды рядов динамики
В зависимости от характеризующего критерия, существует несколько разновидностей динамических рядов.
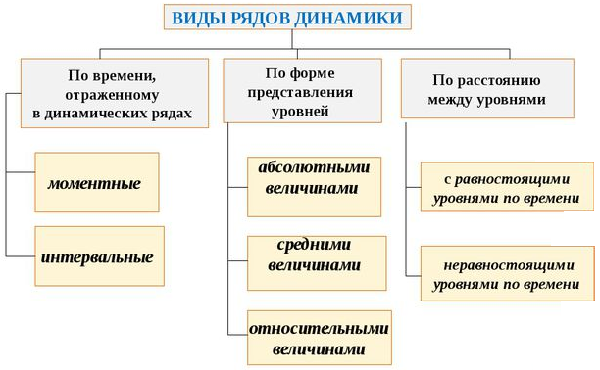
По временной характеристике различают моментальные и интервальные:
- Для интервальных рядов характерна результативность. Иными словами такой ряд может состоять из суммарной характеристики, которая произошла на данный момент времени t (например, сколько продукции произведено на момент времени, сколько человеко-дней зарегистрировано за определенный период).
- Для моментальных рядов характерно мгновенное значение изучаемой характеристики. К таковым относится, например, объем запаса на требуемое время, затраты времени на временной интервал и др.
При характеристике по показателю t выделяют неполные и полные ряды. Неполными считаются такие, в которых не соблюдается одинаковый промежуток между соседними значениями времени. Для полных, такой интервал соблюден.
Кроме этого, существует классификация по количеству показателей. Существуют изолированные – во времени анализируется всего один показатель и многомерные, когда во времени анализ ведется для целого ряда параметров, которые связаны между собой одним процессом.
Правила построения рядов динамики

Когда производится построение временных рядов, то для них должны соблюдаться общие требования:
- Составитель должен придерживаться принципа периодизации развития, когда разбивка на временные этапы должна быть как можно более однородной и подчиняться единому принципу развития. При этом могут использоваться методы параллельной периодизации, многомерного статистического анализа, а также исторический метод.
- Данные, которые объединяются в многомерный временной ряд, должны обеспечивать возможность сопоставления между собой. Иными словами, должен быть определенный общий признак, например, территориальность, единицы измерения и др.
- Временные интервалы должны быть гармонично подобраны в соответствии с вариативностью наблюдаемой характеристики. Это значит, что для величины, которая слишком часто меняет свое значение, интервал должен быть чаще, а для стабильной величины его следует сделать шире.
- Следует соблюдать систематизацию по временной характеристике – не допускать пропуска временных точек, а если таковые возникли, то интерполировать значения внутри пропущенного интервала.
Средние характеристики ряда динамики
Главный показатель, характеризующий среднее значение абсолютных показателей (y1, y2…yn) – это средний уровень ряда. Если основные интервалы не изменялись, то следует пользоваться выражением для расчета (где t – количество уровней):
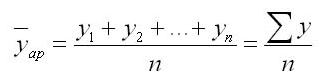
Чуть сложнее будет выглядеть методика расчета, если были временные пропуски или они неравны. Вычисления выполняются через арифметическую взвешенную:
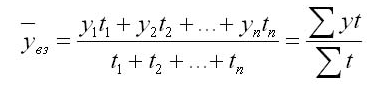
Здесь y1, y2…yn – это абсолютные уровни ряда, а t1, t2…tn – протяженности временных интервалов.
Для описания удобно пользоваться параметром среднего абсолютного прироста, представляющим собой среднее от прироста за равные временные промежутки. Когда использованы гармоничные интервалы, формула выглядит так:
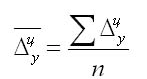
Для приведенного выражения обозначение n – это число приростов за выбранный период.
Также есть методика расчетов с использованием базисного абсолютного прироста при равенстве интервалов для смыкания рядов:
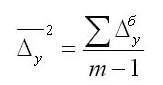
Значение m – это количество уровней в выбранном периоде.
Показательная характеристика средний темп роста, он отображает как происходило изменение уровней рядя (коррелируя с единицами времени). Вычисления для цепных показателей выведены через расчет средней геометрической:
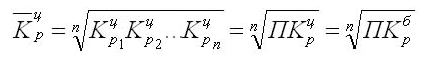
В данном выражении n количество цепных коэффициентов, Кц – сами цепные коэффициенты.
Когда даны все значения уровней, то выражение значительно упрощается:
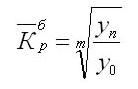
Иногда требуется охарактеризовать срединный темп прироста, рассчитывающийся по уравнению на основании уже известных средних темпов роста (Тр):
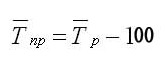
Показатели анализа рядов динамики
Всего имеются 5 характеристик, предназначающихся для выполнения анализа:
- абсолютный прирост – это параметр, получающийся при нахождении разности определенного уровня и базисного (или тем, который следует до него). Возможен ответ со знаком «-». Выражения для расчета выглядят так:
![]()
![]()
- коэффициент роста – значение, которое характеризует, в какое количество раз увеличился (или снизился) конкретно взятый для анализа уровень по сравнению с базисным или любым другим (например, идущим перед выбранным). Формула сводится к делению значения анализируемого уровня на значение базисного (отношение уровней):
![]()
- темп роста – характеризует процентное соотношение анализируемого показателя в сопоставлении с базисным. Вычисления выполняются перемножением значения коэффициента роста на сто процентов,
- темп прироста – процентный порог возрастания или снижения значения уровня в сопоставлении с базисным. При обсчете необходимо из 100 вычесть показатель темпа роста,
- абсолютное значение 1% прироста будет получено при делении абсолютного прироста на темп прироста. Эти характеристики не относятся к обязательным элементам.
Анализ сезонных колебаний
Если взять для анализа временной ряд, в котором собраны объемы продаж противовирусных препаратов за 5 лет, то будет очевидно, что ежегодно происходят колебания (снижение или увеличение) продаж, которые повторяются. Такие колебания будут именоваться сезонными.

Чтобы устранить нежелательное влияние таких колебаний, проводится аналитическое изучение, выполняющееся либо с помощью гармонического исследования, либо с учетом индекса сезонности.
Индекс сезонности это фактическая характеристика того, в какое количество раз анализируемый уровень увеличен или уменьшен относительно срединного:
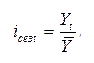
Тут Yt – это уровень, предполагаемый к анализу, а Ȳ это средний уровень всего ряда.
Более сложный анализ предполагает выделение гармонических колебаний. Для этого производится выравнивание по ряду Фурье (так называемые «гармоники»), и высчитывают, какие гармоники наиболее сопоставимы с анализируемым рядом. Общий вид ряда Фурье для двух гармоник выражается формулой:
![]()
Индекс сезонности
Для того чтобы не вычислять относительную разницу в процентах между каждым месяцем во временном ряду, можно вычислить один параметр – индекс сезонности.
Индекс сезонности рассчитывается на основании следующих показателей:
- среднего по анализируемому показателю в указанный временной промежуток за три и более года (yi),
- среднего значения анализируемого показателя внутри одного временного периода (года) – y.
По результатам сопоставления получается значение, которое так или иначе соотносится с уровнем в 100%. Если присутствует значимое отклонение в меньшую сторону, то это является свидетельством присутствия сезонного колебания.
Приведение рядов динамики к одинаковому основанию
Во время работы с несколькими явлениями, описывающими один процесс, может вызывать интерес сопоставление рядов динамики. С целью корректного сопоставления потребуется приведение к одному основанию. Сопутствующей операцией является вычисление коэффициента опережения или отставания.
К каждому ряду находится базисный уровень и вычисляются темпы роста и прироста рядов. Для каждого ряда должен быть выбран аналогичный временной интервал.
Сравнение проводится на основании отношения базисного темпа роста (опционально – прироста) в аналогичном временной интервале. Выражения для расчета достаточно просты:
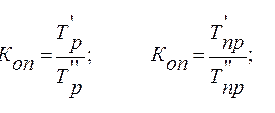
Аналитическое выравнивание ряда динамики
При определении каких-либо закономерностей во временных рядах и возможности прогнозирования отдельных тенденций, применяется методика аналитического выравнивания. С этой целью производится приближение к определенной алгебраической зависимости, наиболее точно описывающей ряд.

Методика укрупнения интервалов представляет собой преобразование, когда временные промежутки делаются более длительными, что позволяет более точно оценить общий вектор тенденции и понять, какое направление будет иметь зависимость.
Методика скользящей средней основана на особенности временных рядов погашать случайные отклонения от среднего уровня. Каждому звену с использованием простого среднеарифметичнского значения нужно рассчитывать уровень, в котором рандомные колебания сведены к минимуму.
Методика аналитического выравнивания под конкретный ряд подбирается зависимость, которая более полно отражает алгебраическую зависимость.
Примеры решения задач на тему «Ряды динамики в статистике»
Классическим упражнением является определение вида и показателей для ряда динамики.
Задача. Для указанного временного ряда высчитать: его вид, цепной и базисный прирост, темп роста/прироста, средний темп прироста.
| Отчетный год | Суммарный объем производства, млрд. руб. |
| 2014 | 18 |
| 2015 | 16 |
| 2016 | 17 |
| 2017 | 16 |
| 2018 | 12 |
Согласно определению, этот ряд динамики относится к интервальному, поскольку в условии приведен четкий промежуток времени. Произведем расчет показателей.
Абсолютные показатели
Абсолютные приросты (по цепному способу):
16 – 18 = 2 млрд. руб.
17 – 16 = 1 млрд. руб.
16 – 17 = 1 млрд. руб.
12 – 16 = 4 млрд. руб.
Абсолютные приросты (по базисному методу):
16 – 18 = -2 млрд. руб.
17 – 18 = 1 млрд. руб.
16 – 18 = -2 млрд. руб.
12 – 18 = 6 млрд. руб.
Относительные показатели
Цепные темпы роста:
16/18 х 100 = 88,8%,
17/16 х 100 = 106%,
16/17 х 100 = 94,1%,
12/16 х 100 = 75%.
Базисные темпы роста:
16/18 х 100 = 88,8%,
17/18 х 100 = 94,4%,
16/18 х 100 = 88,8%,
12/18 х 100 = 66,6%.
Цепные темпы прироста:
-2/18 х 100 = -11,1%,
1/16 х 100 = 6,25%,
-1/17 х 100 = -5,88%,
4/16 х 100 = 25%.
Базисные темпы прироста:
-2/18 х 100 = -11,1%
1/18 х 100 = 5,55%
-2/18 х 100 = -11,1%
-6/18 х 100 = -33,3%
Средний уровень временного ряда:
(18 + 16 + 17 + 16 + 12) / 5 = 15,8.
Среднегодовой абсолютный прирост:
(12 — 18) / (5 — 1) = -1,5 млрд. руб.
Среднегодовой темп прироста:
90.36 – 100 = -9.64%.
Таким образом временные ряды занимают важное место среди статистических объектов.
Основное их преимущество заключается в широком практическом применении, которое позволяет использовать ряды динамики для наблюдений за физическими величинами и экономическими показателями. Важно знать о нюансах, которые помогут правильно проанализировать такие ряды.
