Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин….
Определение параллелограмма
Выпуклый четырехугольник, состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.
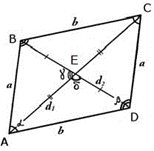
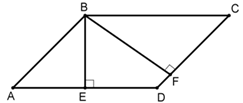
Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.
 |  |
Внимание! Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.
Стороны и углы: особенности соотношения
Ключевые свойства, по большому счету, предопределены самим обозначением, их доказывает теорема. Эти характеристики следующие:
- Стороны, которые являются противоположными, — попарно одинаковые.
- Углы, расположенные противоположно друг другу — попарно равны.
Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).
Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.
Характеристики диагоналей фигуры
Основной признак этих линий параллелограмма: точка пересечения разделяет их пополам.
Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.
AB=CD, так как они противоположные. Согласно правилу параллельных прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.
По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.
Особенности смежных углов
У смежных сторон сумма углов равна 180°, поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:
∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º
Свойства биссектрисы:
- биссектрисы, опущенные на одну сторону, являются перпендикулярными,
- противолежащие вершины имеют параллельные биссектрисы,
- треугольник, полученный проведением биссектрисы, будет равнобедренным.
Определение характерных черт параллелограмма по теореме
Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммом в том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.
Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.
Вычисление площади фигуры
Площадь этой фигуры находится несколькими методами, одним из самых простых: умножения высоты и основания, к которому она проведена.
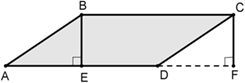
Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF. ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: SABE и SEBCD, а также SDCF и SEBCD. Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:
SABCD = SEBCF = BE×BC=BE×AD.
Для определения общей формулы площади параллелограмма обозначим высоту как hb, а сторону — b. Соответственно:
Другие способы нахождения площади
Вычисления площади через стороны параллелограмма и угол, который они образуют, — второй известный метод.
,
где:
Sпр-ма — площадь,
a и b — его стороны
α — угол между отрезками a и b.
Этот способ практически основывается на первом, но в случае, если высота неизвестна. Перпендикуляр всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть 
. Преобразуя соотношение, получаем 
. В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.
Через диагонали параллелограмма и угол, который они создают при пересечении, также можно найти площадь.
Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.
Площадь каждого из этих ∆ можно найти за выражением 
, где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса. То есть 
. Поскольку AE+CE=AC= d1 и BE+DE=BD= d2, формула площади сводится до:
.
Применение в векторной алгебре
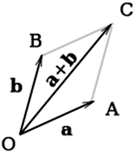
Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы 
и 
не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.
Доказательство: из произвольно выбранного начала — т. о. — строим векторы 
и 
. Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе 
или сумме 
.
Формулы для вычисления параметров параллелограмма
Тождества приведены при следующих условиях:
- a и b, α — стороны и угол между ними,
- d1 и d2 , γ — диагонали и угол в точке их пересечения,
- ha и hb — высоты, опущенные на стороны a и b,
| Параметр | Формула |
| Нахождение сторон | |
| по диагоналям и косинусу угла между ними | 
|
| по диагоналям и стороне | 
|
| через высоту и противоположную вершину | 
|
| Нахождение длины диагоналей | |
| по сторонам и величине вершины между ними | 
|
| по сторонам и одной из диагоналей | 
|
| Нахождение периметра | |
| через стороны |  |
| по диагоналям и стороне |  |
| по стороне, углу между ними и высоте | 
|
| Вычисление площади | |
| при известных сторонах и перпендикуляру из вершины |  |
| по сторонам и углу, который они создают |  |
| по диагоналям и углу, который они создают |  |
Важно! Способов вычисления параметров этой фигуры значительно больше, однако, почти все из них вытекают или из ее свойств, или преобразуются друг из друга.
Геометрия 8 класс. Параллелограмм, свойства параллелограмма
Признаки параллелограмма
Вывод
Параллелограмм как одна из ключевых фигур геометрии находит применение в жизни, например, в строительстве при подсчете площади участка или других измерений. Поэтому знания об отличительных признаках и способах вычисления различных его параметров могут пригодится в любой момент жизни.