Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.
Если 
, то 
.
Логарифм крайне важная математическая величина, поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету….
Свойства логарифмов
Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что 
означает, что:
.
Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.
Приведем некоторые тождества:
,
,
.
Приведем основные алгебраические выражения:
,
,
,
.
Внимание! 
может существовать только при x>,0, x≠1, y>,0.
Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида первый имеет в основании число 10, и носит название десятичный логарифм. Второй называется натуральным. Основание натурального логарифма число е. Именно о нем мы и будем детально говорить в этой статье.
Обозначения:
- lg x десятичный,
- ln x натуральный.
Используя тождество 
можно увидеть, что ln e = 1, как и то, что lg 10=1.
График натурального логарифма
Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его вручную, чтобы знать, как правильно посчитать логарифм.
Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:
| х | у |
| 1 | 0 |
| е | 1 |
| е2≈7,34 | 2 |
 | 0,5 |
| e-1≈0.36 | -1 |
Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: 
. Для натурального логарифма это тождество будет выглядеть таким образом:
.
Для удобства мы можем взять пять опорных точек:
,
,
,
,
.
Как посчитать логарифмы от этих пяти значений? Очень просто, ведь:
,
,
,
,
,
.
Таким образом, подсчет натуральных логарифмов довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.
Построив по точкам график, получаем приблизительный график:
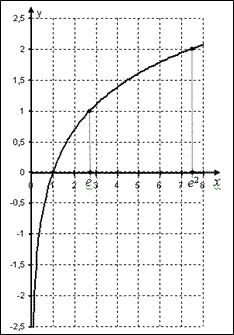
Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) все числа больше нуля.
Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма 
.
Область значений (т.е. все допустимые значения функции y = ln x) все числа в интервале 
.
Предел натурального log
Изучая график, возникает вопрос как ведет себя функция при y<,0.
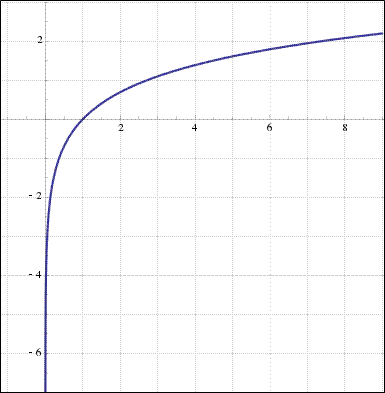
Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х<,0 не существует.
Внимание! При стремлении к нулю аргументу, функция y = ln x стремится к 
(минус бесконечности).
Предел натурального log можно записать таким образом:
Это интересно! Азы геометрии: правильная пирамида — это
Формула замены основания логарифма
Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.
Начнем с логарифмического тождества:
.
Тогда любое число, либо переменную у можно представить в виде:
,
где х любое число (положительное согласно свойствам логарифма).
Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:
.
Воспользуемся свойством (только вместо с у нас выражение):
Отсюда получаем универсальную формулу:
.
В частности, если z=e, то тогда:
.
Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.
Это интересно! Уравнение по трем точкам: как найти вершину параболы, формула
Решаем задачи
Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.
Задача 1. Необходимо решить уравнение ln x = 3.
Решение: Используя определение логарифма: если , то , получаем:
.
Задача 2. Решите уравнение (5 + 3 * ln (x 3)) = 3.
Решение: Используя определение логарифма: если , то , получаем:
.
Тогда:
.
.
Еще раз применим определение логарифма:
.
Таким образом:
.
Можно приближенно вычислить ответ, а можно оставить его и в таком виде.
Задача 3. Решите уравнение 
.
Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:
.
Перед нами квадратное уравнение. Найдем его дискриминант:
.
Первый корень уравнения:
.
Второй корень уравнения:
.
Вспоминая о том, что мы производили подстановку t = ln x, получаем:
.
Используя определение логарифма: если , то , получаем оба корня:
.
Вспомним, что область определения: 
. Оба корня больше нуля, так что оба решения верны и подходят.
Внимание! Когда в логарифмических уравнениях у вас получается два корня или больше, не забывайте про область определения. Аргумент, стоящий под логарифмом никогда не может быть меньше нуля. Если одно из решений делает выражение под логарифмом меньше либо равным нулю такой корень вам не подходит, исключите его.
Интересные сведения
Логарифмы (особенно натуральные и десятичные) широко применимы почти во всех сферах деятельности.
Например, в теории простых чисел, количество простых чисел в интервале от 0 до n будет равно приблизительно: 
, при этом s-ое простое число приблизительно будет равно 
.
В математическом анализе, как мы уже убедились ранее, натуральные логарифмы встречаются сплошь и рядом, при этом они объединяют тригонометрические и логарифмические функции при помощи интегралов, например интеграл от тангенса:
.
В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е зачастую отражает темп роста экспоненциальных величин.
В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти натуральное число N понадобится 
битов.
В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.
В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее процессы, которые математически можно описать только при помощи логарифмирования.
В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.
Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.
Натуральный логарифм Функция y=ln x ее свойства
Доказательство основного свойства натурального логарифма