Основы геометрии: что это такое биссектриса треугольника

Треугольник в геометрии основная фигура, которую нельзя разделить на составляющие. Отрезок прямой линии, соединяющий вершину с противоположной стороной, при условии разделения угла пополам, это биссектриса треугольника. Так как данная фигура содержит 3 угла, соответственно, из каждого можно провести линию, делящую его на равные компоненты.

Свойства биссектрисы

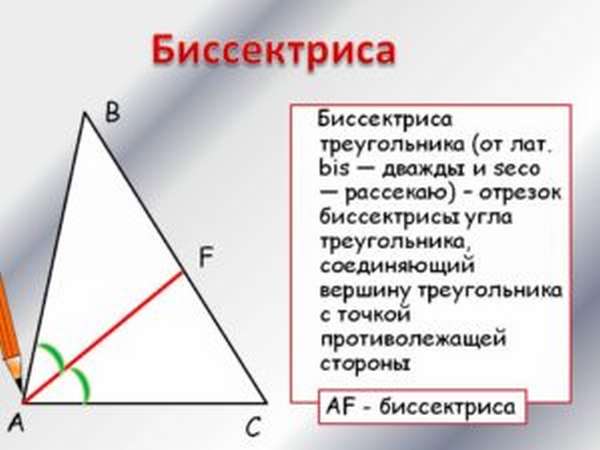Равносторонняя треугольная фигура характеризуется не только равенством сторон, но внутренние углы также одинаковы, при этом они составляют 60° каждый.

Поэтому проведенная биссектриса одновременно является высотой, медианой. Она обладает не только своими качествами, но и характеристиками высоты, медианы треугольника:

• делит противоположные стороны на равные части,
• перпендикулярна к противолежащей стороне,
• в точке пересечения 3 линий каждый отрезок делится в соотношении 2:1, считая от вершины (свойство медианы),
• из центра пересечения можно одновременно провести окружность внутри и вокруг фигуры,
• линии, делящие на равные части внешние углы правильного треугольника, параллельны противоположно расположенным сторонам фигуры,
• все 3 отрезка, проведенные из вершин, равны по длине.

Это интересно! Урок геометрии: как найти по формуле периметр треугольника

Наиболее простая формула, определяющая, как найти биссектрису треугольника, выражается через радиус вписанной (r) или описанной (R) окружности:

• l=3r,
• l=3R/2.

Характеристика внутренних линий

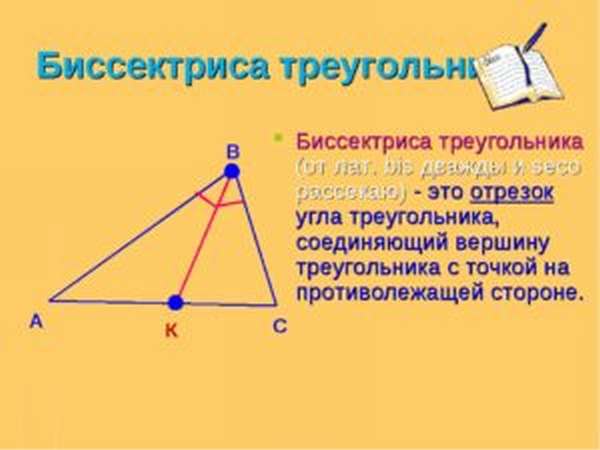Основное свойство биссектрисы треугольника с равными боковинами: отрезок, опущенный из вершины, одновременно является медианой, высотой.

При этом, кроме разделения угла на 2 равные части, линия характеризуется следующими качествами:

• делит нижнее основание пополам,
• служит перпендикуляром к противолежащей стороне,
• отрезок луча, разделяющий внешний угол вершины с равными боковинами, параллелен основанию.

Важно! Биссектрисы равных углов у основания также равны между собой по длине.

При этом верно обратное утверждение: когда 2 биссектрисы равны между собой, то треугольник считается равнобедренным.

Если вершина содержит 90° (прямой угол), то отрезки, опущенные на катеты, пересекаются под 45°. В этом случае определить размер искомого отрезка помогает теорема Пифагора.

Это интересно! Что значит вертикально и как выглядит вертикальная линия

Пример

В треугольнике АВС вершина А содержит 90°. Отрезок АД служит высотой, биссектрисой и медианой одновременно. Образованы 2 прямоугольные трехсторонние фигуры: АВД и АСД, у которых равны основания (ВД=СД). Требуется найти длину отрезка АД.

По теореме Пифагора АД2 = АВ2-ВД2. Отсюда АД = √АВ2-ВД2.

Это интересно! Изучаем символы: как обозначается в математике площадь

Соотношение со сторонами треугольника

Слово, в переводе с латинского языка, обозначает «сечение поперек». Чем отличается биссектриса от других главных и второстепенных отрезков треугольной фигуры, было известно еще Архимеду, который в своих трудах активно использовал ее свойства для определения сторон многоугольников. При этом количество сторон должно быть кратным трем. Классическая теорема о биссектрисе гласит, что линия разделяет противоположную сторону на 2 отрезка, отношение которых друг к другу такое же, как соотношение двух соприкасающихся к основанию сторон.

Пример

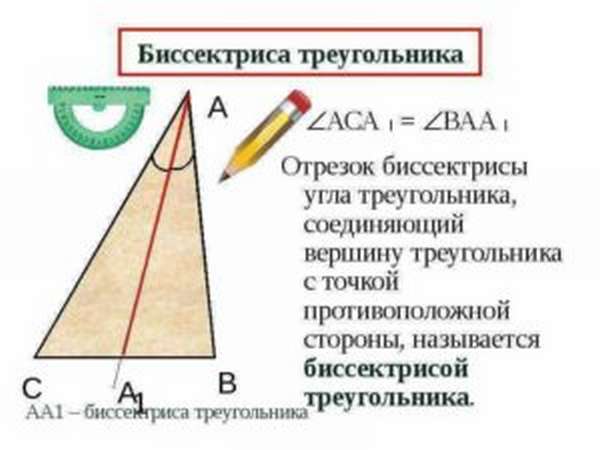Дан треугольник АВС. Из вершины А проведена биссектриса АД, разделяющая сторону ВС на 2 отрезка (ДВ и ДС). Смысл теоремы сводится к равенству нескольких величин: ВД/АВ=СД/АС и ВД/ДС=АВ/АС. Лучше понять формулу помогает фото треугольника с проведенной линией.

Характеристика линий:

• любая биссектриса, выпущенная из вершины неправильного треугольника, расположена между медианой и высотой, выходящей из этого же места,
• все точки, расположенные на отрезке, удалены от сторон по бокам вершины на одинаковое расстояние,
• лучи, разделяющие пополам внешний и внутренний угол треугольной фигуры, перпендикулярны между собой,
• все отрезки, делящие на равные части внутренние углы, пересекаются в строго определенной точке, которая служит центром вписанной в эту фигуру окружности,
• если две биссектрисы равны по длине, то фигура – равнобедренная, если все одинакового размера, треугольник – правильный.

Способы построения

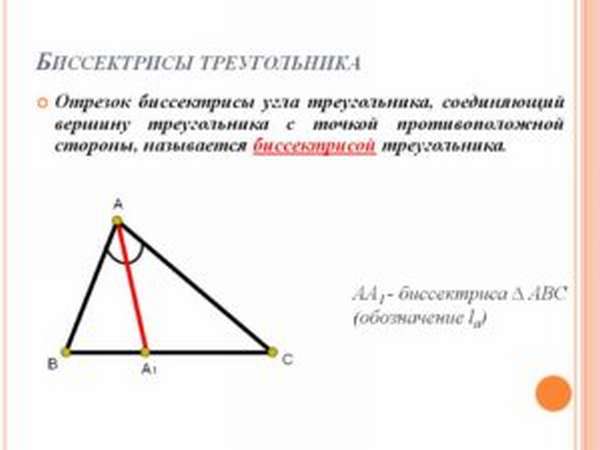Зная, что такое биссектриса, легко определить расположение отрезка в треугольной фигуре. Для построения применяется несколько способов:

1. Известен угол, из которого исходит прямая, делящая его на равные сегменты. Значение делится пополам. На рисунке с помощью транспортира строится нужный отрезок.
2. Если параметры угла неизвестны, его измеряют транспортиром, делят пополам, затем проводят искомую линию.
3. Оригинальный способ построить нужный отрезок с помощью карандаша, линейки и циркуля. Из любой вершины проводится окружность произвольного радиуса. Главное, что величина должна быть меньше, чем прилегающая сторона. Место пересечения с каждой стороной считается центром для еще двух окружностей с таким же шагом циркуля. Нарисовать еще два круга, которые пересекаются между собой два раза. Через полученные точки и вершину под линейку проводится прямая, которая и есть настоящая биссектриса внутреннего угла.
4. Построить треугольник по известной длине трех отрезков (АВ, ВС, АС) можно с помощью линейки и циркуля. На произвольной прямой линии обозначить сегмент, равный АВ. Из точки А провести окружность с шагом циркуля равным АС, а затем аналогично из точки В провести окружность с шагом ВС. Точка пересечения – вершина искомой треугольной фигуры (С), в которой легко определяются биссектрисы, учитывая их характеристики.

Важно! Если известны только размеры биссектрис, то построить по данным параметрам возможно бесконечное количество подобных фигур.

Полезное видео

Подведем итоги

Зная значение и характеристики главных линий в треугольной фигуре, можно решать много задач, определять величину углов, длину, изучать соотношение сторон.