С целью повышения точности решения практических задач, как в строительстве, так и экономике иногда нужен более «мощный» инструмент, который давал бы ответ на нестандартные условия. К примеру, вычисление площади покрытия не традиционной формы (половины параболы), изготовление конструкций, удаляемая или застраивая площадь и многое другое. Таким инструментом является именно интеграл, рамки исчисления которого, задает сам пользователь. Приведем примеры вычислений определенного интеграла с доказательством его свойств,
Значение понятия
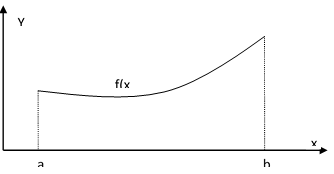
Рисунок 1. Общий вид криволинейной трапеции.
Невзирая на теоретическое обоснование, сразу дадим более четкое понятие этого термина. Определенным интегралом считается площадь криволинейной трапеции, которая за основания принимает снизу – ось абсцисс, а снизу саму функцию. Более наглядно это изображено на рисунке 1. Такое трактование называется геометрическим, и более понятно, чем остальные.
В более классическом определении, численное выражение интеграла является величина какой – либо первообразной на выбранном и ограниченном промежутке (отрезке). На практике значение такого приращения может быть, как больше, так и меньше нуля. В отношении значения площади данный вопрос зависит от того, в какой полуплоскости находится кривая (верхней или нижней), такой и будет знак (на практике его значение отбрасывают). В численном выражение наше определение имеет такую формулу:
![]()
Опираясь на вышеуказанную формулу можем утверждать, что определенный интеграл представляет собой разность первообразной в крайних точках выбранного интервала (такой подход к определению называют формула Ньютона – Лейбница).
Это интересно! Первый признак равенства треугольников: доказательство
Свойства интеграла Римана на отрезке
Для того, чтобы безошибочно находить площади «кривых» трапеций, рассмотрим основные «приёмы», которые существенно облегчат этот процесс.
Основные свойства:
Площадь трапеции в отдельно взятой точке равна нулю. Формулой можно записать так:
![]()
Если функция определена между точками a и b, то справедливо следующее равенство:
![]()
Если под интегральные функции w(x) и t(x) определены на отрезке [k,c] и не имеют точек разрыва, нет таких точек в которых бы функции не имели значения, то справедливо равенство:
![]()
В случае если первообразная функция определена (вычислима в каждой точке) и пределы интегрирования лежат на отрезке [k,c], тогда под интегральную функцию можно записать в следующем виде:
![]()
Функция j(x) интегрируема на отрезке [a,d], только в том случае, когда сам отрезок [a,d] принадлежит большему отрезку [k,c].
Отметим, что данный список не включает в себя все свойства определенного интеграла и имеет продолжение. Указанные «хитрости» являются наиболее распространенными приемами, однако применять их нужно убедившись в их «работоспособности».
Для большей наглядности найдем значение интеграла, пределы интегрирования которого расположены на отрезке [3,5] для под интегральной
![]()
Решение. Согласно условию задачи, имеем следующую под интегральную функцию определенную на промежутке
![]()
Можем получить следующее:
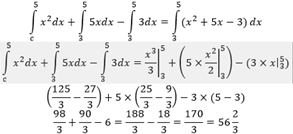
Получается, что площадь криволинейной трапеции будет составлять ., вполне очевидно, что можно было и сразу взять определенный интеграл от заданной функции не прибегая к использованию свойства, однако такой подход более точно раскрывает возможности одного из свойств.
Допустим, что вместо функции с переменной x, находится 0 (такой вариант тоже считают функцией и совпадает с осью абсцисс). Тогда пытаясь найти определённый интеграл от постоянной получим:
![]()
Выходит, что если в под интегральной функции стоит нуль, то и первообразная, на каком бы отрезке не была определена, тоже будет равна нулю.
В случае, если требуется найти интеграл от константы, то следующее решение дает пример решения любого многочлена:
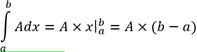
Откуда делаем вывод, что если требуется определить интеграл от нуля, то его значение (можно даже не расписывать) равен нулю, а если интеграл от числа, то разницу между концами отрезка нужно умножить на число под знаком интеграла.
Важно! Во время решения задач подобного плана, часто приходится комбинировать указанные приемы, для уменьшения сложности задания. Но используя такие переходы, не стоит забывать, что интегральная сумма всегда должна совпадать с первоначальной. Всегда проверяйте отрезок, на котором собираетесь интегрировать, иначе полученное значение будет отличаться от действительного.
«Умные» определения интегрирования непрерывной функции
Для удачного поиска первообразной необходимо знание и понимание таких понятий как: интегральная сумма, пределы интегрирования и общее понимание определения «интеграл функции».
Границы на определенном отрезке
Суть данного понятия заключается в том, что пределы интегрирования функции (это тот самый отрезок, который заранее определяется), это максимально граничные значения кривой, в которых она еще «действительна». К примеру, наша под интегральная определена на отрезке от 2 до 4. Это означает что мы можем найти первообразную для функции в точке со значением 2.000000001 (практически 2) и 3.9999999 (почти 4), но если пределы интегрирования больше (меньше), то все дальнейшие значения бессмысленны. Изобразим это на рисунке 2, где предложены возможные продолжения кривой.
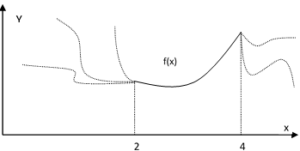
Рисунок 2.Возможное поведение функции за пределами интегрирования.
Такое требование к пределам вытекает из того, что нам не известно определена ли функция за этими пределами или нет. А также то, как она поведет себя за своими пределами. По сути, функция верхнего основания говорит о том, как располагаются точки на указанном отрезке (вполне возможно, что за пределами это уже будет функция Дирихле, то есть будут точки разрыва). В своей сущности под понятием «интеграл функции» имеется в виду процесс поиска первообразной (первородной), из которой эта самая функция при поиске производной и получилась. Еще проще – действие обратное поиску производной.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
Сумма
Представим, что дана произвольная трапеция, верхнее основание которой произвольная кривая. Если из образованной фигуры, образовать похожие внутри первоначальной. То получим бесконечное множество таких трапеций, у каждой из которых функция, определяющая верхнее основание, будет одинакова. Далее на каждом нижнем основании (малые отрезки) возьмём какую угодно точку, умножим значение функции в этой самой точке на разницу в основании, то получим площадь этой трапеции. Сумма площадей всех этих трапеций, будет равна площади изначально данной. Это будет интегральная сумма.
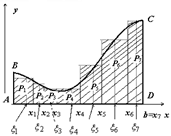
Рисунок 3. Сумма интегралов.
Математически это будет выглядеть так:

Для более понятного восприятия рекомендуем присмотреться к рисунку 3.
Полезное видео: что такое определенный интеграл?
Полезное видео: как решить определенный интеграл?
Вывод
При решении обычных задач или примеров данные определения редко имеют существенное значение. Но не лишним будет их правильное понимание и применение перед тем, как начнется само решение. Как правило, определенные интегралы, представляемые на ЕГЭ, все соответствуют данным критерием. Однако, теория проверяется тоже, и не стоит её отбрасывать ввиду сложности понимания.
Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения
