Огромный блок математики посвящен работе с дробями или нецелыми числами. С ними очень часто встречаются и в жизни, поэтому знать, как работать с такими цифрами важно для любого человека. Математика – это наука, в которой ученик начинает с познания простых вещей и действий, а затем переходит к более сложным….
Знание и умение работать с подобными цифрами облегчит ему в дальнейшем работу с логарифмами, рациональными показателями и интегралами. С такими числами можно делать все то же самое, что и с обыкновенными: складывать дроби, делить, вычитать и умножать. Кроме этого, их можно сокращать. Работать с дробями просто, главное – это знать основные правила и методы их вычисления.
Основные понятия
Для того, чтобы понять, что это за значение такое, необходимо представить некий целый предмет. Допустим, что есть торт, который порезали на несколько одинаковых или равных кусков. Каждый кусочек будет называться долей.
Важно! В случае с дробями, есть некое целое число, которое состоит из равных долей – отдельных меньших чисел.
Например, 10 состоит из 5 двоек, каждая двойка – это часть от десяти.
Доли имеют свои названия, в зависимости от их общего количества в целом числе: 10 может состоять из двух пятёрок или пяти двоек, в первом случае она будет называться (одна вторая)
, а во втором 
(одна пятая). Следует помнить, что равняется половине числа, 
(одна третья) трети, а 
(одна четвертая) – четвертью. Их могут также изображать через черточку: ½, 1/3 или 1/5.
Цифру, написанную сверху горизонтальной линии или слева от наклонной, называют числителем – он показывает сколько долей взяли у целого числа, а цифра под линии или справа от нее – знаменатель, он показывает на сколько всего долей разделили. Например, торт разделили на 10 кусков и сразу отложили два из них для опоздавших гостей. Это будет 2/10 (две десятых), т.е. взяли 2 (числитель) куска от общих 10 (знаменатель).
Дроби
Какие бывают доли, что такое неправильная дробь, что такое обыкновенная дробь? На эти вопросы легко ответить:
- Обыкновенная – это такая, в котором числитель и знаменатель являются натуральными числами и записываются так:
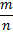или m/n, - Правильная дробь – это такая, которая по своей величине меньше единицы, а числитель меньше знаменателя: 5/7 (пять седьмых), 3/5 (три пятых),
- Неправильная – это такая, которая больше или равна единице, а ее знаменатель меньше или равен числителю: 7/5 (семь пятых) или 19/3 (девятнадцать третьих),
- Смешанная – это состоящая из целого и доли: 2
(две целых три пятых) или 5
(пять целых шесть двенадцатых) .
Смешанная цифра всегда может трансформироваться в неправильную дробь и наоборот.
Главное свойство гласит: при умножении, а также деления делимого и делителя на одинаковый множитель, в целом величина дроби не изменится. Это свойство делает возможным все операции с дробями.
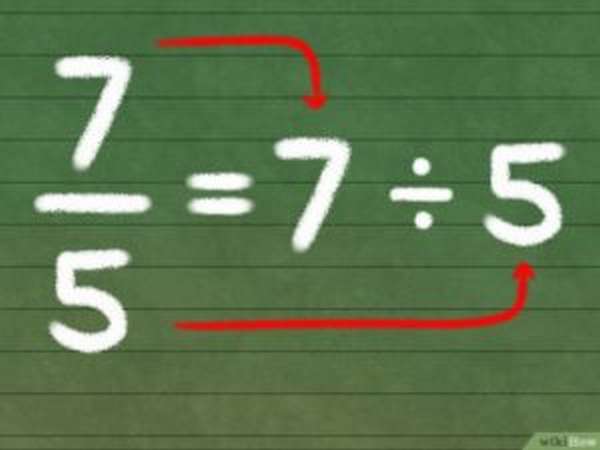Как из неправильной дроби сделать правильную
Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения
Как сократить?
Главное правило гласит, что долевую цифру можно сократить поделить ее числитель и знаменатель на одинаковый делитель (отличный от 0) так, чтобы получилась новая цифра с меньшими параметрами, но равная исходной по величине. Исходя из этого правила можно понять, что дроби бывают сократимые и несократимые.
Пример сокращения дробей: 8/24 сократим, поделив ее параметры на 2. Получим: 8:2=4 и 24:2=12. В результате, исходная цифра превратится в 4/12 . Можно повторить операцию, вновь поделив числа: 4:2=2 и 12:2=6. Получим 2/6. Еще раз повторим операцию: 2:2=1 и 6:2=3. В итоге получится несократимая цифра 1/3, поскольку ее параметры уже нельзя разделить на одинаковый делитель. Любое сократимое число можно привести к несократимому.
Важно ! Если делимое или делитель представлены выражением 
(, вначале каждое из выражений надо умножить на один множитель и дробь превратить в простую, сократив на этот множитель выражение: 
.
Сокращать можно при умножении дробных выражений друг на друга: 
*
. Сами по себе эти числа несократимые, но выполняя операцию умножения, можно сократить их по диагонали:
*
=
=
. Сокращать при умножении можно только крест-накрест: числитель первой со знаменателем второй, и наоборот.
Сокращать можно и смешанную цифру, т.е. целую часть и правильную дробь представить в виде неправильной. Для этого следует выполнить некоторые действия:
- Имея 5
, преобразуем его в неправильную дробь. Для этого знаменатель перемножим с его целой частью и приплюсуем к полученной цифре числитель: 5*9+1=46, - Сумма станет числителем неправильной доли, а его низ позаимствуем от первоначальной,
- В итоге получаем:
.
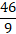Справедливо и обратное действие: из неправильной дроби сделать смешанную. Для этого рассмотрим обратное действие с :
- Разделим между собой верх и низ: 46:9=5,111111111111111,
- Целый результат деления станет полной цифрой, а бесконечный остаток – верхом доли,
- Знаменатель при этом останется неизмененным,
- Получаем 5.
Таким способом сокращать дроби при любых операциях возможно. Можно сокращать значения ее делимого и делителя при умножении их на одинаковый множитель, и превращая из смешанного числа в долю, и наоборот.
Сокращение дробей
Возможные действия
Все основные виды вычислений доступны при счете долей, как и с целыми цифрами: сложение, вычитание и прочие. Рассмотрим каждое действие по отдельности с примерами:
Сложение и вычитание
Складывать доли можно двумя путями, в зависимости от их делителя. Они бывают одинаковыми и разными. Рассмотрим пример складывания долей с одинаковыми делителями.
Для решения 
+ необходимо по отдельности сложить делимое долей, а делитель не трогать: 1+1. Результатом станет цифра 
, но поскольку она неправильная, то ее можно преобразовать в смешанную, разделив делимое на делитель: 2:2= 1. Неправильную долю всегда (!) следует приводить к правильной и несокращаемой, т. е. если ее делимое и делитель можно поделить на одинаковый множитель – это следует сделать в обязательно порядке.
В случае сложения долей с различными делителями, их необходимо изначально привести к одинаковому. Например, для решения : 
необходимо:
- Найти наименьшее общее кратное (НОК) для делителей. Здесь у делителей 2 и 3 меньшее кратное – 6.
- НОК делят вначале на первый делитель, а затем на второй: 6:3=2 и 6:3=2. В данном случае полученные 2 и 3 – это первый и второй дополнительные множители.
- Каждое слагаемое первоначального примера умножить на найденные множители:
+ 
=
+ 
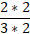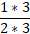. - Далее складываем доли:
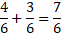. - Преобразуем: 1
.
Вычитание осуществляется точно так же: в случае с одинаковыми делителями их не трогаем, а числители последовательно вычитаем: 
= 
=
. Если же знаменатели различные, то следует поступить, как и при сложении: найти НОК, множители, умножить доли, а затем вычесть уже доли с одинаковыми делителями.
Сложение дробей
Умножение и деление
При умножении необходимо последовательно перемножить их верх и низ между собой: 
= поскольку есть возможность сокращения на 6. В случае деления все несколько сложнее.
Для деления 
следует:
- Умножить первый множитель на долю, обратную второй, т. е.
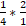, - Далее действует правило умножения:
=
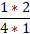= , поскольку первоначальный результат можно сократить на 2.
Важно! Деление всегда можно заменить умножением, но только при соблюдении условия замены делителя на обратное ему число.
Перевод смешанного числа в неправильную дробь
Выделение целой части из неправильной дроби
Чтобы правильно решать подобные примеры, следует запомнить главное свойство и правила сокращения. Что касается операций, то важно знать, как правильно складывать и умножать при одинаковых и разных знаменателях, поскольку делятся и вычитаются они по одинаковому принципу.