 В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени. Именно они помогают учёным в изучении внешней среды и её использовании.
В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени. Именно они помогают учёным в изучении внешней среды и её использовании.
Квадратные уравнения
Квадратным называется равенство вида ax² + bc + c = 0, где x является переменой, a (первый коэффициент), b (второй) и c (свободный) — это действительные числа, которые должны приводить в условии задачи. Нужно помнить при решении, что a ≠ 0. Как уже понятно, оно очень отличается от линейного уравнения, его все изучали в младших классах школы.
Чтобы понять, как решать квадратные уравнения, нужно представить футбольное поле, длина которого на 10 метров больше его ширины, а площадь равна 380 квадратных метров. Нужно найти ширину футбольного поля.
Пусть переменная x — это определённая ширина, тогда её длина будет (х +10) метров. Потом x * (x + 10) = 380, ведь дана площадь 380 квадратных метров в условии задачи, то есть x² + 10x 380 равно нулю. Здесь а = 1, b = 10, а c = -375 Это был один из примеров квадратных равенств.
Различают два вида уравнений:
- Приведённые — это случай, когда в квадратном равенстве a = 1.
- Непривёденные если a ≠ 1.
При этом x² — приведённое, а уже при 5x² оно станет непривёденным.
Понятие дискриминант
Существует определенная система решения таких уравнений. Чтобы найти чётный корень такого равенства, достаточно запомнить приведённую ниже формулу квадратного уравнения.
Буква D — это дискриминант. Звучит сложно, но не стоит пугаться, ведь с латинского языка слово переводится, как разность. Он равен: D = b² 4 ac. Следуя этому, можно записать, что (2ax + b)² = D. Есть определенные правила, как надо решать дискриминант:
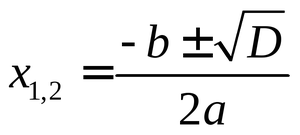 Если D меньше нуля, то действительных корней нет.
Если D меньше нуля, то действительных корней нет.- В случае когда D равняется нулю, в решении получается только один действительный корень, но есть редкие случаи с двумя, то есть можно писать при решении в формуле либо +, либо -.
- Если D больше нуля, то в уравнении два действительных корня, то есть и плюс, и минус. Но чтобы укоротить решение достаточно записать ±, вместо двух вариантов решения задачи.
Пример первого способа нахождения через формулу дискриминанта квадратного уравнения и правильным разложением чисел:
- 9х²-6х+1=0,
- D = (-6)² 4 × 9 ×1 = 0,
- D эквивалентен нулю,
- x = -6/2×9 = 1/3.
Как пример можно показать уравнивание: -8x² = 0, у которого b и с равны нулю. Или 2x² 3 = 0, b ничему не равно. В уравнении -7x² + 4x² = 0 c эквивалентно нулю.
Разные квадратные уравнения
 Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² 4 ac = 4 (k² ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.
Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² 4 ac = 4 (k² ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.
Квадратные равенства с комплексными переменными почти ничем не отличаются от плоскости действительных чисел и тем, которые должны проходить в восьмых классах. И чтобы без проблем их решать, нужно использовать формулу.
Если в квадратном равенстве хотя бы один из общих коэффициентов квадратного трехчлена B или C равен нулю, то такое равенство называют неполным.
Следовательно оно бывает только трёх видов:
 Уравнение вида ax² равно нулю. Поскольку а ≠ 0, имеем случай, когда x² = 0, корнем которого есть число ноль. Как уже понятно, имеется единственный корень х равен нулю.
Уравнение вида ax² равно нулю. Поскольку а ≠ 0, имеем случай, когда x² = 0, корнем которого есть число ноль. Как уже понятно, имеется единственный корень х равен нулю.- ax² + c равно нулю, тогда с не будет равняться нулю. Чтобы это лучше понять, приводится уравнение ах² = -c, x² = -c/a. Поскольку c ≠ 0 тогда и -с/а также не равно нулю. Если -с/а больше нуля, то получается два корня: х1 = корень из -с/а и ещё х2 = корень из с/а. Также можно написать вместо минуса и плюса одно уравнение из знаком: ±. Возможен случай, когда ситуация является обратной (-с/а <, 0), тогда корней совсем нет. Пример: -2х² + 50 равняется нулю. -2х²= -50, х² = 25, х1,2 = ±5.
- ах² + bx = 0, и при этом b нулю не равно. Разложим левую часть уравнения на множители и решим полученное х * (ах + b) = 0. Ответ: x равен нулю или ax + b = 0, но x = -b/a, поскольку a ≠ 0. В итоге должно выйти два корня: х1 = 0 и х2 = -b/a. Один из примеров: 2х² + 5х эквивалентен нулю, х(2х+ 5) = 0, х= 0 или 2х + 5 = 0. На данный момент очевидно, что x2 = -2,5 и х1 эквивалентен нулю.
Из истории математики
 Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.
Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.
Это показал древнегреческий учёный Диофант. Много внимания таким уравнениям также выделял арабский математик Мухаммед Альхорезми. Он нашёл как решать уравнение видов: ах²=bx, ax²=c, ax²+bx=c, ax²+c=bx, bc+c=ax² и получил положительные корни.
Формулы, что связывают между собой корни равенства и его коэффициенты, впервые нашёл французский математик Франсуа Виет в 1591 году. Его заключения в современных обозначениях имеют вид: (а + b)x x² = 0.
После быстрой публикации работы нидерландского математика Жераром, а также француза Декарда и англичанина Ньютона равенство корней квадратного уравнения приобрело современный вид.
| Уравнения | х1 и х2 | х1+х2 | х1×х2 |
| х² -6х + 8 = 0 | 2 и 4 | 6 | 8 |
| x²+x-12=0 | -4 и 3 | -1 | -12 |
| x²-4x-5=0 | -3 и -2 | -5 | 6 |
| x²-4x-5=0 | -1 и 5 | 4 | -5 |
Сейчас речь идёт о теореме Виета, на которую нужно обратить внимание. Её так называют из-за известного французского математика Франсуа Виета, которым и было открыто это свойство. Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.
Теорему можно сформулировать так.
Если х1 и х2 — корни сведенного квадратного равенства х²+px+q эквивалентны нулю, то х1 + х2 = -p, x1 * x2 = q. Поскольку a ≠ 0, поделим две части уравнения на а и получается современная формула: x² b/a * x + c/a равно нулю.
